概念
1.朴素贝叶斯
朴素贝叶斯是为数不多的基于概率论的分类算法。朴素贝叶斯原理简单,也很容易实现,多用于文本分类,比如垃圾邮件过滤。
算法思想——基于概率的预测
逻辑回归通过拟合曲线(或者学习超平面)实现分类,决策树通过寻找最佳划分特征进而学习样本路径实现分类,支持向量机通过寻找分类超平面进而最大化类别间隔实现分类。相比之下,朴素贝叶斯独辟蹊径,通过考虑特征概率来预测分类。
理论基础——条件概率,词集模型、词袋模型
- 条件概率:朴素贝叶斯最核心的部分是贝叶斯法则,而贝叶斯法则的基石是条件概率。贝叶斯法则如下 \(p(c_{i}|x,y)=\frac{p(x,y|c_{i})p(c_{i})}{p(x,y)}\)
这里的C表示类别,输入待判断数据,式子给出要求解的某一类的概率。我们的最终目的是比较各类别的概率值大小, 而上面式子的分母是不变的,因此只要计算分子即可。
- 词集模型:对于给定文档,只统计某个侮辱性词汇(准确说是词条)是否在本文档出现
- 词袋模型:对于给定文档,统计某个侮辱性词汇在本文当中出现的频率,除此之外,往往还需要剔除重要性极低的高频词和停用词。因此,词袋模型更精炼,也更有效。
| 为了高效计算,求解P(x,y | C0)时是向量化操作的,因此不会一个个的求解P(xn,yn | C0)。 |
1 算法流程
以敏感文档识别为例:
首先,我们需要一张词典,该词典囊括了训练文档集中的所有必要词汇(无用高频词和停用词除外),还需要把每个文档剔除高频词和停用词;
其次,根据词典向量化每个处理后的文档。具体的,每个文档都定义为词典大小,分别遍历某类(敏感和非敏感)文档中的每个词汇并统计出现次数;最后,得到一个个跟词典一样大小的向量,这些向量由一个个整数组成,每个整数代表了词典上一个对应位置的词在当下文档中的出现频率。
| 最后,统计每一类处理过的文档中词汇总个数,某一个文档的词频向量除以相应类别的词汇总个数,即得到相应的条件概率,如P(x,y | C0)。有了P(x,y | C0)和P(C0),P(C0 | x,y)就得到了,用完全一样的方法可以获得P(C1 | x,y)。比较它们的大小,即可知道某篇文档是不是敏感文档了。 |
2 优点
- 朴素贝叶斯模型发源于古典数学理论,有稳定的分类效率。
- 对小规模的数据表现很好,能个处理多分类任务,适合增量式训练,尤其是数据量超出内存时,我们可以一批批的去增量训练。
- 对缺失数据不太敏感,算法也比较简单,常用于文本分类。
3 缺点
- 理论上,朴素贝叶斯模型与其他分类方法相比具有最小的误差率。但是实际上并非总是如此,这是因为朴素贝叶斯模型假设属性之间相互独立,这个假设在实际应用中往往是不成立的,在属性个数比较多或者属性之间相关性较大时,分类效果不好。而在属性相关性较小时,朴素贝叶斯性能最为良好。对于这一点,有半朴素贝叶斯之类的算法通过考虑部分关联性适度改进。
- 需要知道先验概率,且先验概率很多时候取决于假设,假设的模型可以有很多种,因此在某些时候会由于假设的先验模型的原因导致预测效果不佳。
- 由于我们是通过先验和数据来决定后验的概率从而决定分类,所以分类决策存在一定的错误率。
- 对输入数据的表达形式很敏感。
2.半朴素贝叶斯分类器
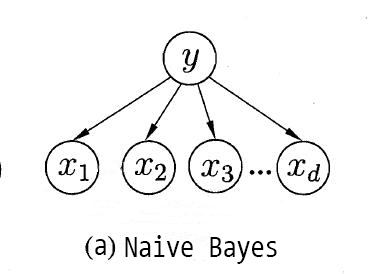
朴素贝叶斯分类器基于属性条件独立性假设,每个属性仅依赖于类别,如上图。但这个假设往往很难成立的,有时候属性之间会存在依赖关系,这时我们就需要对属性条件独立性假设适度地进行放松,适当考虑一部分属性间的相互依赖信息,这就是半朴素贝叶斯分类器(semi-naive Bayes classifier)的基本思想。
独依赖估计(One-Dependent Estimator,简称ODE)是半朴素贝叶斯分类器最常用的一种策略,它假设的是每个属性在类别之外最多仅依赖于一个其他属性。也即:
\[P(c\ |\ \mathbf{x}) \propto P(c) \prod_{i=1}^{d} P(x_i\ |\ c,{pa}_i)\]其中 ${pa}_i$ 是属性 $x_i$ 依赖的另一属性,称为 $x_i$ 的父属性。若已知父属性,就可以按式(5)来计算了。现在问题转化为如何确定每个属性的父属性?
这里介绍两种产生独依赖分类器的方法:
SPODE
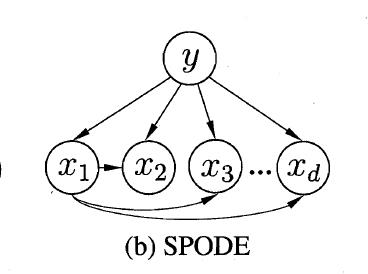
在SPODE(Super-Parent ODE)中,所有属性都依赖于一个共同的属性,称为超父(super-parent),比方说上图中的 $x_1$。可以通过交叉验证等模型选择方法来确定最合适的超父属性。
TAN
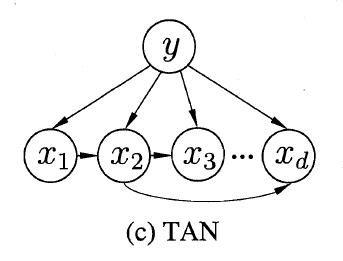
TAN(Tree augmented naive Bayes)则是一种基于最大带权生成树(maximum weighted spanning tree)的方法,包含以下四个步骤:
-
计算任意两个属性间的条件互信息(conditional mutual information):
\(I(x_i,x_j\ |\ y) = \sum_{x_i,x_j; c\in \mathcal{Y}} P(x_i,x_j\ |\ c) \log \frac{ P(x_i,x_j\ |\ c)}{ P(x_i\ |\ c) P(x_j\ |\ c)}\) -
以属性为节点构建完全图,每条边的权重为对应的条件户信息。
-
构建此完全图的最大带权生成树。选一个节点作为根节点,把边转换为有向边。
-
加入类别节点 $y$,并增加从 $y$ 到每个属性的有向边。
AODE
特别地,有一种更为强大的独依赖分类器——AODE(Average One-Dependent Estimator),它基于集成学习机制。无须通过模型选择来确定超父属性,而是尝试将每个属性都作为超父属性来构建模型,然后把有足够训练数据支撑的SPODE模型集成起来导出最终结果。
类似于朴素贝叶斯分类器,AODE无需进行模型选择,既可以通过预计算来节省预测时间,又可以采取懒惰学习,需要预测时再进行计数,并且可以容易地实现增量学习。
高阶依赖
ODE假设每个属性最多依赖类别以外的另一属性,但如果我们继续放宽条件,允许属性最多依赖类别以外的 k 个其他属性,也即考虑属性间的高阶依赖,那就得到了 kDE。
| 是不是考虑了高阶依赖就一定能带来性能提升呢?并不是这样的。随着 k 的增加,要准确估计条件概率 $P(x_i\ | \ c,\mathbf{pa}_i)$ 所需的训练样本会呈指数上升。如果训练样本不够,很容易陷入高阶联合概率的泥沼;但如果训练样本非常充足,那就有可能带来泛化性能的提升。 |
贝叶斯网
贝叶斯网(Bayesian network)亦称信念网(belief network),它借助有向无环图(Directed Acyclic Graph,简称DAG)来刻画属性之间的依赖关系,并使用条件概率表(Conditional Probability Table,简称CPT)来描述属性的联合概率分布。
贝叶斯网的学习包括结构的学习和参数的学习,而预测新样本的过程则称为推断(inference)。这部分内容设计到一些后面章节,相对复杂一些,所以暂且放下,之后有时间再写详细的笔记。
3.Gaussian Naive Bayes
\[P(x_{i}|y)=\frac{1}{\sqrt{2\pi \sigma_{y}^{2}}}exp(-\frac{(x_{i}-\mu _{y})^{2}}{2\sigma _{y}^{2}})\]4.EM算法
前面讨论的极大似然估计方法是一种常用的参数估计方法,它是假设分布的形式,然后用训练样本来估计分布的参数。但实际任务中,我们遇到一个很大的问题就是训练样本不完整。这时就需要用到EM(Expectation-Maximization)算法了。
所谓不完整的样本,说的是这个样本某些属性的值缺失了。将每个属性的取值看为一个变量,那么缺失的就可以看作“未观测”变量,比方说有的西瓜根蒂脱落了,没办法看出根蒂是“蜷缩”还是“硬挺”,那么这个西瓜样本的根蒂属性取值就是一个“未观测”变量,更准确地说,称作隐变量(latent variable)。
整个训练集可以划分为已观测变量集 $X$ 和隐变量集 $Z$ 两部分。按照极大似然的思路,我们依然是想找出令训练集被观测到的概率最大的参数 $\Theta$。也即最大化对数似然:
\[LL(\Theta\ |\ X,Z) = \ln P(X,Z\ |\ \Theta)\]但是,由于 $Z$ 是隐变量,我们没办法观测到,所以上面这个式子实际是没法求的。
怎么办呢?EM算法的思路很简单,步骤如下:
- 设定一个初始的 $\Theta$
- 按当前的 $\Theta$ 推断隐变量 $Z$ 的(期望)值
- 基于已观测变量 $X$ 和 步骤2得到的 $Z$ 对 $\Theta$ 做最大似然估计得到新的 $\Theta$
- 若未收敛(比方说新的 $\Theta$ 与旧的 $\Theta$ 相差仍大于阈值),就回到步骤2,否则停止迭代
EM算法可以看作是用坐标下降(coordinate descent)法来最大化对数似然下界的过程,每次固定 $Z$ 或者 $\Theta$ 中的一个去优化另一个,直到最后收敛到局部最优解。
理论上,用梯度下降也能求解带隐变量的参数估计问题,但按我的理解,由于隐变量的加入,使得求导这个步骤非常困难,计算也会随着隐变量数目上升而更加复杂,EM算法避免了这些麻烦。
scikit-learn示例
在scikit-learn中,提供了3中朴素贝叶斯分类算法:GaussianNB(高斯朴素贝叶斯)、MultinomialNB(多项式朴素贝叶斯)、BernoulliNB(伯努利朴素贝叶斯)
import numpy as np
X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
Y = np.array([1, 1, 1, 2, 2, 2])
from sklearn.naive_bayes import GaussianNB
clf = GaussianNB()#默认priors=None
clf.fit(X, Y)
#priors属性:获取各个类标记对应的先验概率
#clf.set_params(priors=[0.625, 0.375])
GaussianNB(priors=None)
print(clf.predict([[-0.8, -1]]))
#
clf_pf = GaussianNB()
clf_pf.partial_fit(X, Y, np.unique(Y))
GaussianNB(priors=None)
print(clf_pf.predict([[-0.8, -1]]))
[1]
[1]
版权声明:本文为博主原创文章,转载请注明出处。 旭日酒馆