Python 中的方法解析顺序（Method Resolution Order, MRO）定义了多继承存在时 Python 解释器查找函数解析的正确方式。当 Python 版本从 2.2 发展到 2.3 再到现在的 Python 3，MRO算法也随之发生了相应的变化。这种变化在很多时候影响了我们使用不同版本 Python 编程的过程。

MRO

class A():
    def who_am_i(self):
        print("I am A")
        
class B(A):
    pass
        
class C(A):
    def who_am_i(self):
        print("I am C")

class D(B,C):
    pass
    
d = D()

d.who_am_i()

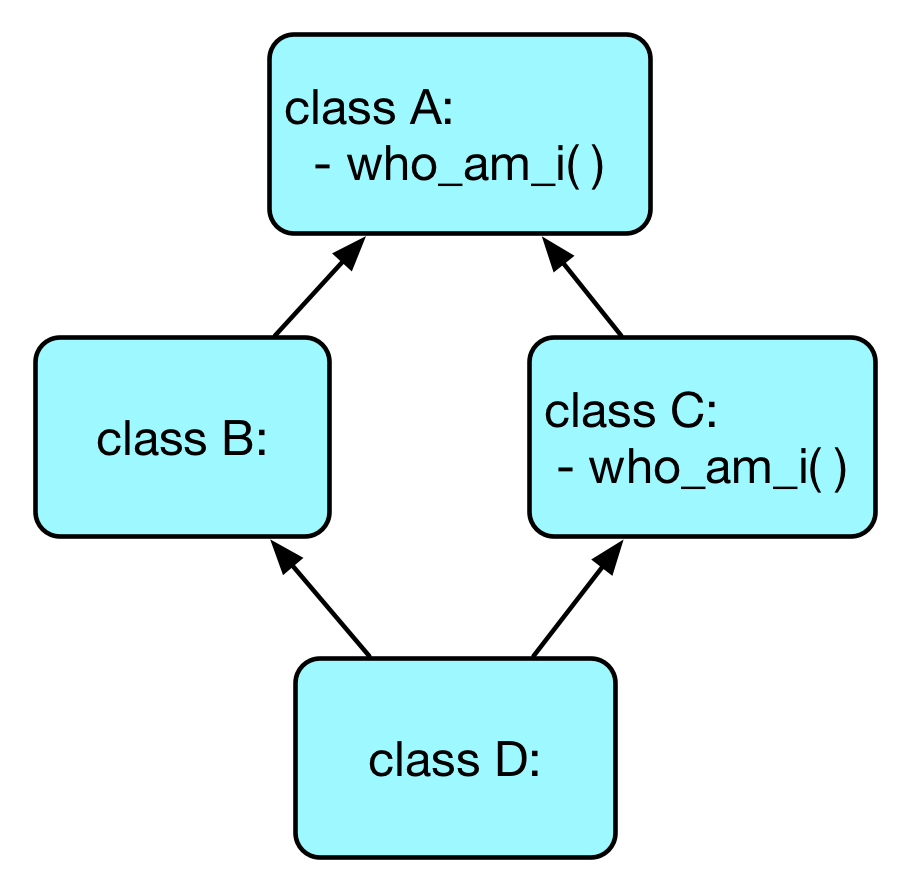
上述代码究竟执行的是 A 中的 who_am_i() 还是 C 中的 who_am_i()呢？

• 在 Python 2 中使用 D 的实例调用 d.who_am_i()，

• 在 Python 3 中使用的是 C 中的 who_am_i()，

MRO决定基类中的函数到底应该以什么样的顺序调用父类中的函数。Python 发展到现在，MRO 算法已经不是一个凭借着执行结果就能猜出来的算法了。如果没有深入了解 MRO 算法的细节，在使用多重继承时难免遇到一些莫名其妙的问题。

Old-style Class

在 Python 2.1 及以前，定义一个类的时候往往是这个样子（我们把这种类称为 old-style class)：

class A:
    def __init__(self):
        pass

• old-style class 的 MRO

Python 2 对于 old-style class 使用了非常简单的基于深度优先遍历的 MRO 算法。当一个类继承自多个类时，Python 2 按照从左到右的顺序深度遍历类的继承图，从而确定类中函数的调用顺序。这个过程具体如下：

检查当前的类里面是否有该函数，如果有则直接调用。

检查当前类的第一个父类里面是否有该函数，如果没有则检查父类的第一个父类是否有该函数，以此递归深度遍历。

如果没有则回溯一层，检查下一个父类里面是否有该函数并按照 2 中的方式递归。

上面的过程与标准的深度优先遍历只有一点细微的差别：步骤 2 总是按照继承列表中类的先后顺序来选择分支的遍历顺序。具体来说，类 D 的继承列表中类顺序为 B, C，因此，类 D 按照先遍历 B 分支再遍历 C 分支的顺序来确定 MRO。

在 Python 2 中，通过如下方式来查看 old-style class 的 MRO：

>>> import inspect
>>> inspect.getmro(D)

可以看到函数 d.who_am_i() 调用的搜索顺序是 D, B, A, C, A。由于一个类不能两次出现，因此在搜索路径中去除掉重复出现的 A，得到最终的方法解析顺序是 D, B, A, C。所以打印的是 I am A 。

New-style Class

Python 2.2 引入了新的模型对象（new-style class），其建议新的类型通过如下方式定义：

class A(object):
    def __init__(self):
        pass

• new-style class 的 MRO

new-style class 定义方式显示注明类 A 继承自 object,Python 2.3 及后续版本为了保持向下兼容，同时提供以上两种类定义用以区分 old-style class 和 new-style class。Python 3 则完全废弃了 old-style class 的概念，不论通过以上哪种方式书写代码，Python 3 都将明确认为类 A 继承自 object

可以感觉到，使用深度优先遍历的查找算法并不合理。因此，Python 3 以及 Python 2 针对 new-style class 采用了新的 MRO 算法。

使用 Python 3 运行上述脚本，可以看到函数 d.who_am_i() 的打印结果是 I am C。

在 Python 3 中，通过如下方式来查看 new-style class 的 MRO：

>>> D.mro()
(<class 'test.D'>, <class 'test.B'>, <class 'test.C'>, <class 'test.A'>, <class 'object'>)

新算法与基于深度遍历的算法类似，但是不同在于新算法会对深度优先遍历得到的搜索路径进行额外的检查。其从左到右扫描得到的搜索路径，对于每一个节点解释器都会判断该节点是不是好的节点。如果不是好的节点，那么将其从当前的搜索路径中移除。我们说 N 是一个好的节点*当且仅当搜索路径中 N 之后的节点都不继承自 N.

以上述的类继承图为例，按照深度优先遍历得到类 D 中函数的搜索路径 D, B, A, C, A。之后 Python 解释器从左向右检查时发现第三个节点 A 不是一个好的节点，因为 A 之后的节点 C 继承自 A。因此其将 A 从搜索路径中移除，然后得到最后的调用顺序 D, B, C, A。

采用上述算法，D 中的函数调用将优先查找其直接父类 B 和 C 中的相应函数。

这个算法有一个明确的名字 C3 linearization。其形式化的计算过程如下：

在介绍算法之前，我们首先约定需要使用的符号。我们用 C1C2⋯CN表示包含 N 个类的列表，并令

head(C1C2⋯CN)=C1

tail(C1C2⋯CN)=C2C3⋯CN

为了方便做列表连接操作，我们记：C1+(C2C3⋯CN)=C1C2⋯CN

假设类 C继承自父类 B1,⋯,BN，那么根据 C3 线性化，类 C的方法解析列表通过如下公式确定：

L[C(B1⋯BN)]=C+merge(L[B1],⋯,L[BN],B1⋯BN)

这个公式表明 C的解析列表是通过对其所有父类的解析列表及其父类一起做 merge操作所得到。

接下来我们介绍 C3 线性化中最重要的操作 merge，该操作可以分为以下几个步骤：

1. 选取 merge中的第一个列表记为当前列表 K。

2. 令 h=head(K)，如果 h 没有出现在其他任何列表的 tail 当中，那么将其加入到类 C 的线性化列表中，并将其从 merge中所有列表中移除，之后重复步骤 2。

3. 否则，设置 K为 merge中的下一个列表，并重复 2 中的操作。

4. 如果 merge中所有的类都被移除，则输出类创建成功；如果不能找到下一个 h，则输出拒绝创建类 C 并抛出异常。

C3 linearization的做法类似 拓扑排序 Topological Sorting

new-style MRO的例子

>>> O = object
>>> class F(O): pass
>>> class E(O): pass
>>> class D(O): pass
>>> class C(D,F): pass
>>> class B(D,E): pass
>>> class A(B,C): pass

• L[C]

计算方法：

L[C] = L[C(D, F)]
     = C + merge(L[D], L[F], DF)
     # 从前面可知 L[D] 和 L[F] 的结果
     = C +  merge(DO, FO, DF)
     # 因为 D 是顺序第一个并且在几个包含 D 的 list 中是 head，
     # 所以这一次取 D 同时从列表中删除 D
     = C + D + merge(O, FO, F)
     # 因为 O 虽然是顺序第一个但在其他 list (FO)中不是 head, 跳过,
     # 改为检查第二个list FO # F 是第二个 list 和其他 list 的 head, 
     # 取 F同时从列表中删除 F
     = C + D + F + merge(O)
     = C D F O

验证：

>>> C.mro()
[<class '__main__.C'>, <class '__main__.D'>, <class '__main__.F'>, <type 'object'>]

• L[B]

与L[C]同样的，

>>> B.mro()
[<class '__main__.B'>, <class '__main__.D'>, <class '__main__.E'>, <type 'object'>]

• L[A]

L[A]有些复杂了，计算方法如下：

L[A] = L[A(B, C)]
     = A + merge(L(B), L(C), BC)
     = A + merge(BDEO, CDFO, BC)
     = A + B + merge(DEO, CDFO, C)
     # 注意这里是 C , 因为第一个list 的 head D 不是其他list 的 head
     # 所以改为从下一个 list CDFO 开始
     = A + B + C + merge(DEO, DFO)
     = A + B + C + D + merge(EO, FO)
     = A + B + C  + D + E + merge(O, FO)
     = A + B + C + D + E + F + merge(O)
     = A B C D E F O

验证：

>>> A.mro()
[<class '__main__.A'>, <class '__main__.B'>, <class '__main__.C'>,
 <class '__main__.D'>, <class '__main__.E'>, <class '__main__.F'>, <type 'object'>]

参考

The Python 2.3 Method Resolution Order

版权声明：本文为博主原创文章，转载请注明出处。 旭日酒馆

• 编程 (8)

• python (4) ,
• MRO (1) ,
• 多重继承 (1)