1 常见概念
- 数据(data):为了描述和解释所搜集、分析、汇总的事实和数字
- 数据集(data set):用于特定研究而搜集的所有数据
- 个体(element):搜集数据的实体
- 变量(variable):个体中所感 兴趣的那些特征
- 观测值(observation):包含个体和变量的测量值集合
- 测量尺度:
- 名义尺度(nominal scale):数值代码及非数字标记
- 顺序尺度(ordinal scale):有序的
- 间隔尺度(interval scale):顺序数据,并可按某一固定度量单位表示数值间的间隔。永远是数值型的
- 比率尺度(ratio scale):间隔数据,且两个数值之比有意义
- 数据类型:
- 分类型数据(categorical data)和分类变量(categorical variable)
- 数量型数据(quantitative data)和数量变量(quantitative variable)
- 按数据搜集时期分类:
- 截面数据(cross-sectional data):在相同或挖相同的同一时点上搜集的数据
- 时间序列数据(time series data):在多个时期内搜集的数据
- 描述统计(descriptive statistics):以表格、图形或数值形式汇总的统计方法
- 统计推断(statistical inference):利用样本数据对总体特征进行估计和假设检验
- 总体(population)
- 普查(census):搜集总体全部数据的调查过程
- 样本(sample)
- 抽样调查(sample survey):搜集样本数据的调查过程
逻辑分析方法(analytics):
- 描述性分析(descriptive analytics):描述过去生发状况的分析技术
- 数据查询
- 报告
- 描述统计
- 数据可视化
- 数据仪表板
- “如果xxx,则xxx”型电子表格模型
- 预测性分析(predictive analytics):利用过去数据建立的模型来预测未来的分析技术
- 线性回归
- 时间序列分析
- 预测模型
- 规范性分析(prescriptive analytics):产生一个最佳行动过程的分析技术集合
- 在一组约束条件下产生最大或最小目标的解决方案的优化模型
2 描述统计学:表格法和图形法
汇总数据的表格法和图形法:
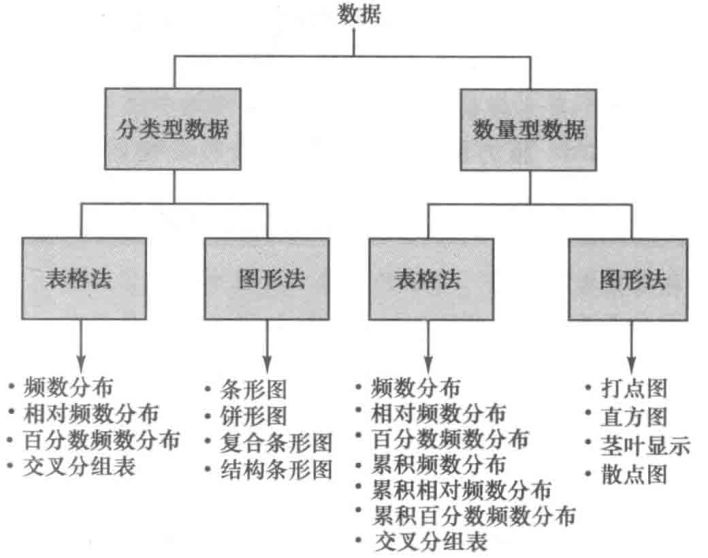
- 汇总分类变量的数据
- 频数分布(frequency distribution)
- 相对频数分布(relative frequency distribution):对一个有n个观测值的数据集, $每一组的相对频数=(组的频数/n)$
- 百分数频数分布(percent frequency distribution):百分比化的相对频数
- 条形图(bar chart)
- 饼形图(pie chart)
- 频数分布(frequency distribution)
- 汇总数量变量的数据
- 频数分布
- 组数:建议使用5-20组
- 组宽:建议每组的宽度相同, $近似组宽=(数据最大值-数据最小值)/组数$
- 组限:使每一个数据值只属于一组,有上组限和下组限
- 组中值(class midpoint):下组限和上组限的中间值
- 打点图(dot plot)
- 直方图(histogram)
- 累积频数分布(cumulative frequency distrubution):表示小于或等于每一组上组限的数据项个数
- 累积相对频数分布(cumulative relative frequency distrubution)
- 累积百分数频数分布(cumulative percent frequency distrubution)
- 茎叶显示(stem-and-leaf display):同时显示数据的等级排序和分布形态
- 频数分布
- 用表格方法汇总两个变量的数据
- 交叉分组表(crosstabulation)
- 常见的是一个变量是分类,而另一个变量是数量的两个变量数据
- 若是两个数量变量时,需对变量值分组
- 辛普森悖论(Simpson’s paradox):依据综合和未综合数据得到相反结论
- 注意交叉分组表是综合形式还是未综合形式,特别要审查是否存在可能影响结论的隐藏变量
- 交叉分组表(crosstabulation)
- 用图形显示方法汇总两个变量的数据
- 散点图(scatter diagram):对两个数量变量间关系的图形表述
- 趋势线(trendline):显示相关性挖程度的一条直线
- 复合条形图(side-by-side bar chart):同时显示多个已汇总的条形图
- 结构条形图(stacked chart):堆叠
数据可视化:创建有效图形显示的最佳实践
- 清晰、简明的标题
- 简洁,能用二维表示时就不用三维图形
- 每个坐标轴有清楚的标记,并给出测量单位
- 使用对比明显的颜色区分类别
- 图例要靠近所表示的数据
- 选择恰当的图形类型
- 展示数据分布:条形图、饼形图、打点图、直方图、茎叶显示
- 比较:复合条形图、结构条形图
- 展示相关关系:散点图、趋势线
- 数据仪表盘要最大限度减少屏幕滚动,避免不必要的颜色和三维显示,图与图之间要有边框,以提高可读性
3 描述统计学:数值方法
常见样本统计量和总体参数符号:

- 位置的度量
- 平均数(mean)
- 样本平均数: $\bar{x} =\frac{\sum x_{i}}{n}$
- 总体平均数: $\bar{\mu } =\frac{\sum x_{i}}{N}$
- 加权平均数:$\bar{x} =\frac{\sum w_{i}x_{i}}{w_{i}}$ ,其中 $w_{i}$ 为第i个观测值的权重
- 中位数(median)
- 对奇数个观测值,中位数是中间的数值
- 对偶数个观测值,中位数是中间两个数值的平均值
- 几何平均数(geometric mean): $\bar{x} {g}=\sqrt[n]{x{1}x_{2}…x_{n}}=(x_{1}x_{2}…x_{n})^{1/n }$
- 常用于分析财务数据的增长率
- 众数(mode):出现次数最多的数据
- 百分位数(percentile)
- 第p百分位数,是指大约有p%的观测值比第p百分位数小,大约有1-p%的观测值比第p百分位数大
- 第p百分位数位置: $L_{p} =\frac{p}{100} (n+1)$
- 四分位数(quartiles):$Q_{1}$ =25%的观测值,$Q_{2}$ =50%的观测值,$Q_{3}$ =75%的观测值
- 百分位数(percentile)
- 平均数(mean)
- 变异程度(即离散程度)的度量
- 极差(range)=最大值-最小值
- 四分位数间距(interquartile range,IQR): $IQR=Q_{3} -Q_{1}$
- 方差(variance)
- 离差(deviation about the mean):$x_{i}-\bar{x}$
- 样本方差(sample variance):$s^{2} =\frac{\sum (x_{i}-\bar{x})^{2} }{n-1}$
- 总体方差(sample variance):$\sigma ^{2} =\frac{\sum (x_{i}-\mu )^{2} }{N}$
- 标准差(standard deviation):方差的正平方根
- 标准差和原始数据的单位度量相同,更容易与平均数等统计量进行比较
- 常用于度量与股票和基金投资相关的风险,给出了月回报率围绕长期平均回报率波动的度量
- 标准差系数(coefficient of variation):$(\frac{标准差}{平均数}\times100 )\%$
- 标准差相对于平均数大小的描述
- 分布形态、相对位置的度量及异常值检测
- 偏度(skewness):对称、左偏、右偏
- z-分数(z-score):数值的相对位置,$z_{i} =\frac{x_{i}-\bar{x} }{s}$
- 表示 $x_{i}$比样本平均数大$z_{i}$个标准差
- 切比雪夫定理(Chebyshev’s theorem):与平均数的距离在z个标准差之内的数据值所占的比例至少为$1-\frac{1}{z^{2}}$
- 至少75%的数据值与平均数据的距离在z=2个标准差之内
- 至少89%的数据值与平均数据的距离在z=3个标准差之内
- 至少94%的数据值与平均数据的距离在z=4个标准差之内
- 经验法则(empirical rule):适用于正态分布
- 大约68%的数据值与平均数的距离在1个标准差之内
- 大约95%的数据值与平均数的距离在2个标准差之内
- 几乎所有的数据值与平均数的距离在3个标准差之内
- 异常值(outliers)
- 通常将z-分类小于-3和大于3的数值视为异常值
- 基于IQR确定正常数据的上限和下限,超出上限和下限的视为异常值
- $下限=Q_{1}-1.5\times IQR$
- $上限=Q_{3}+1.5\times IQR$
- 五数概括法(five-number summary)
- 最小值
- 第一四分位数$Q_(1)$
- 中位数$Q_(2)$
- 第三四分位数$Q_(3)$
- 最大值
- 箱形图(box plot):基于五数概括法的数据图形汇总
- 可列出多个箱形图进行比较分析
- 两变量间关系的度量
- 协方差(covariance): $s_{xy}=\frac{\sum (x_{i}-\bar{x})(y_{i}-\bar{y}) }{n-1}$
- 样本协方差的解释:
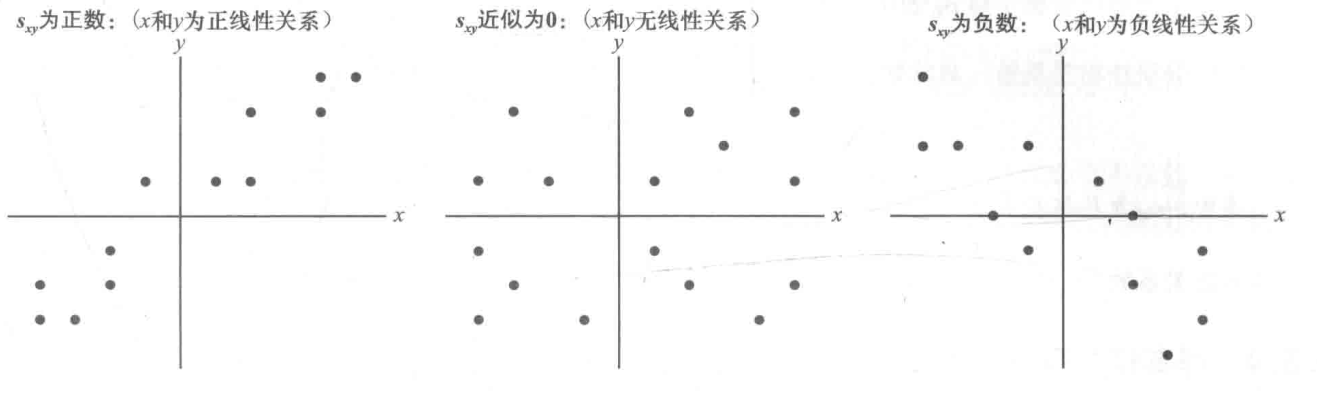
- 相关系数(correlation coefficient):量度两变量间的相关关系
- 样本数据的皮尔逊积矩相关系数: $r_{xy}=\frac{s_{xy}}{s_{x}s_{y}}$
- 相关系数仅度量两个数据变量之间线性相关关系的强度
- 非线性关系的两个变量之间,相关系数可能接近于0,表明没有线性关系
4 概率
随机实验:所产生的试验结果是完全确定的(样本空间(sample space),常用S表示)。在每一次重复或实验中,出现哪种结果(样本点(sample point))完全由偶然性决定。
计数法则:
- 多步骤实验(multiple-step experiment)计数法则:如果一个实验有循序的k个步骤,第1步有$n_{1}$种实验结果,第2步有$n_{2}$种实验结果,第k步有$n_{k}$种实验结果,则实验结果的总数为$n_{1}\times n_{2}\times…\times n_{k}$
- 树形图(tree diagram)可用于帮助分析多步骤实验
- 组合计数法则:从N项中任取n项的组合数为:$C_{n}^{N} =\binom{N}{n} =\frac{N!}{n!(N-n)!}$,其中,$N!=N\times (N-1)\times (N-2)\times …\times 2\times 1$,$n!=n\times (n-1)\times (n-2)\times …\times 2\times 1$,并且定义$0!=1$
- 排列计数法则:从N项中任取n项的排列数为:$P_{n}^{N} =n!\binom{N}{n} =\frac{N!}{(N-n)!}$
概率分配的两个基本条件:
- 每个实验结果的概率值都必须在0和1之间
- 所有试验结果的概率之和必须为1
| 概率分配方法 | 适用场景 |
|---|---|
| 古典法(classical method) | 适用于各种试验结果是等概率发生的场景 |
| 相对频率法(relative frequency method) | 适用于可大量重复实验,并能取得试验结果发生频率的数据 |
| 主观法(subjective method) | 适用于不能假定试验结果是等可能发生的,或无法取得相关数据时 |
事件(event):样本点的一个集合。
事件的概率:事件中所有样本点的概率之和。
概率的基本性质:
- 事件的补(complement of A,$A^{c}$):$P(A)+P(A^c)=1$
- 加法公式:$P(A\cup B)=P(A)+P(B)-P(A\cap B)$
- 事件A和事件B的交(intersection of A and B):$A\cap B$
- 事件A和事件B的并(union of A and B):$A\cup B$
- 互斥事件(mutually exclusive events)没有公共的样本点,是一种特例,$P(A\cup B)=P(A)+P(B)$
-
乘法公式(multiplication law):$P(A\cap B)=P(B)P(A B)$或$P(A\cap B)=P(A)P(B A)$
| 条件概率(conditional probability,$P(A | B)$):在事件B已经发生的条件下考虑A发生的可能性 |
-
$P(A B)=\frac{P(A\cap B)}{P(B)}$ -
$P(B A)=\frac{P(A\cap B)}{P(A)}$ -
独立事件,即:$P(A B)=P(A)$且$P(B A)=P(B)$
贝叶斯定理(Bayes’s theorem):从一个初始的先验概率(prior probability),根据新增信息计算修正概率,更新先验概率得到后验概率(posterior probability)。
- 两事件情形的贝叶斯定理
-
$P(A_{1} B)=\frac{P(A_{1})P(B A_{1})}{P(A_{1})P(B A_{1})+P(A_{2})P(B A_{2})}$ -
$P(A_{2} B)=\frac{P(A_{2})P(B A_{2})}{P(A_{1})P(B A_{1})+P(A_{2})P(B A_{2})}$
-
- 希望计算后验概率的事件是互斥的,且它们的并构成了整个样本空间
-
$P(A_{i} B)=\frac{P(A_{i})P(B A_{i})}{P(A_{1})P(B A_{1})+P(A_{2})P(B A_{2})+…+P(A_{n})P(B A_{n})}$
-
- 表格法:依次计算事件的先验概率、条件概率、联合概率和后验概率
5 离散型概率分布
随机变量(random variable)是对试验结果的数值描述。
- 离散型随机变量(discrete rndom variable):可取有限多个值或无限可数多个值
- 离散型随机变量的数学期望(随机变量中心位置的度量):$E(x)=\mu =\sum xf(x)$
- 离散型随机变量的方差(随机变量的变异性或分散程度度量):$Var(x)=\sigma ^2=\sum (x-\mu )^2f(x)$
- 离散型随机变量的标准差(随机变量的变异性或分散程度度量):$\sigma =\sqrt{Var(x)}$
-
连续型随机变量(continuous random variable):可取某一区间或多个区间内任意值
- 离散型概率分布的概率函数(probability function,$f(x)$)
- 基本条件:$f(x)\ge 0$且$\sum f(x)=1$
- 离散型均匀概率函数:$f(x)=1/n$
- 关于两个随机变量的概率分布称为二元概率分布(bivariate probability distribution),也称作联合概率
- 随机变量x和y的协方差:$\sigma _{xy}=\left [ Var(x+y)-Var(x)-Var(y) \right ] /2$
- 随机变量x和y的相关系数:$\rho _{xy}=\frac{\sigma _{xy}}{\sigma _{x}\sigma _{y}}$
- 随机变量x和y的线性组合的数据期望:$E(ax+by)=aE(x)+bE(y)$
- 随机变量x和y的线性组合的方差:$Var(ax+by)=a^2Var(x)+b^2Var(y)+2ab\sigma _{xy}$
二项概率分布(binomial probability distribution)
二项试验的四个性质:
- 试验由一系列相同的n个试验组成
- 每次试验有两种可能的结果
- 每次试验成功的概率都是相同的:p=1-p
- 试验是相互独立的
同时满足后三条性质,即该实验是由伯努利过程产生的。四条性质同时满足,则称其为二项试验,相应的概率分布为二项概率分布:如,抛硬币
- 二项概率函数:$f(x)=\binom{n}{x} p^x(1-p)^{(n-x)}$
- 二项分布的数学期望:$E(x)=\mu =np$
- 二项分布的方差:$Var(x)=\sigma ^2=np(1-p)$
泊松概率分布(Poisson probability distribution)
泊松试验的两个性质:
- 在任意两个相等长度的区间上,事件发生的概率相等
- 事件在某一区间上是否发生,与事件在其他区间上是否发生是独立的
泊松概率函数:$f(x)=\frac{\mu ^xe^{-\mu}}{x!}$
超几何概率分布(hypergeometric probability distribution)
与二项分布的不同:
- 各次试验不是独立的
- 各次实验中成功的概率不等
超几何概率函数:$f(x)=\frac{\binom{r}{x} \binom{N-r}{n-x} }{\binom{N}{n} }$
- 用于计算n个元素中恰好有x个元素具有成功标志,n-x个元素具有失败标志的概率
- N:总体中元素个数
- n:试验次数
- x:成功次数
- r:总体中具有成功标志的元素个数
6 连续型概率分布
概率密度函数(probability density function,f(x)):给定区间上区线f(x)下的面积是连续型随机变量在该区间取值的概率。
均匀概率分布(uniform probability distribution)
- 均匀概率密度函数:$f(x)=\frac{1}{b-a}$,当$a\le x\le b$时;$f(x)=0$,在其他情况下
- 均匀概率分布的期望:$E(x)=\frac{a+b}{2}$
- 均匀概率分布的方差:$Var(x)=\frac{(b-a)^2}{12}$
正态概率分布(normal probability distribution)
- 正态概率密度函数:$f(x)=\frac{1}{\sqrt{2\pi \sigma } } e^{-(x-\mu)^2/2\sigma ^2 }$
- 标准正态概率分布(standard normal probability distribution):随机变量服从均值为0,标准差为1的正态分布
- 标准正态概率密度函数:$f(x)=\frac{1}{\sqrt{2\pi} } e^{-z^2/2 }$
- 将具有均值$\mu$和标准差$\sigma$的正态随机变量x转换为标准正态随机变量$z$的公式:$z=\frac{x-\mu }{\sigma }$
- 二项概率的正态近似:连续性校正因子(continuity correction factor)
指数概率分布(exponential probability distribution)
- 数概率密度函数:$f(x)=\frac{1}{\mu } e^{-x/\mu}$,$x\ge 0$
- 指数分布的累计概率:$P(x\le x_{0})=1-e^{-x_{0}/\mu}$
泊松分布描述了每一区间中事件发生的次数,指数分布描述了事件发生的时间间隔长度。
7 抽样和抽样分布
- 样总体(sampled population):从目标总体(target population)中抽取样本的总体
- 抽样框(frame):用于抽选样本的个体清单
选取样本:
- 从有限总体的抽样
- 简单随机样本:各样本以相等的概率被抽出,无放回抽样更为常用
- 从无限总体的抽样:随机样本(random sample)
- 条件1:抽取的每个个体来自同一总体
- 条件2:每个个体的抽取是独立的
利用样本去推断总体时,应确保所设计的研究中,抽样总体与目标总体是高度一致的。抽样总体参数与点估计值差异应可预期。
点估计值(point estimate):用于估计总体参数的样本统计量。
- 样本均值$\bar{x}$是总体均值$\mu$的估计
- 样本标准差$s$是总体标准差$\sigma$的估计
- 样本比率$\bar{p}$是总体比率$p$的估计
抽样分布(sample distribution):$\bar{x}$,是样本均值$\bar{x}$与总体均值$\mu$的接近程度的概率度量。
$\bar{x}$的数学期望:$E(\bar{x})=\mu$。
当点估计量的期望值等于总体参数时,我们称这个点估计量是无偏的(unbiased)。
$\bar{x}$的抽样分布
$\bar{x}$的标准差:
- 有限总体:$\sigma _{\bar{x}}=\sqrt{\frac{N-n}{N-1} } \frac{\sigma }{\sqrt{n} }$
- 有限总体修正系数(finite population correction factor):$\sqrt{\frac{N-n}{N-1} }$
- 无限总体:$\sigma _{\bar{x}}=\frac{\sigma}{\sqrt{n} }$
$\bar{x}$的抽样分布形式:
- 总体服从正态分布
- 总体不服从正态分布
- 中心极限定理(central limit theorem):从总体中抽取容量为n的简单随机样本,当样本容量很大时,样本均值$\bar{x}$的抽样分布近似服从正态分布
$\bar{p}$的抽样分布
- 计算公式:$\bar{p}=x/n$
- $\bar{p}$的数据期望:$E(\bar{p})=p$
- $\bar{p}$的标准差:
- 有限总体:$\sigma _{\bar{p}}=\sqrt{\frac{N-n}{N-1} } \sqrt{\frac{p(1-p)}{n} }$
- 如果总体是有限的,且$n/N> 0.05$,需要采用有限总体修正系数
- 无限总体:$\sigma _{\bar{p}}= \sqrt{\frac{p(1-p)}{n} }$
- 有限总体:$\sigma _{\bar{p}}=\sqrt{\frac{N-n}{N-1} } \sqrt{\frac{p(1-p)}{n} }$
当$np\ge 5$,且$n(1-p)\ge 5$时,$\bar{p}$的抽样分布可用正态分布近似。
点估计的性质
- 无偏性
- 有效性
- 一致性
其他抽样方法
- 分层随机抽样(stratified random sampling)
- 整群抽样(cluster sampling)
- 系统抽样(systemematic sampling)
- 方便抽样(convenience sampling)
- 判断抽样(judgment sampling)
8 区间估计
- 边际误差(marginal of error)
- 区间估计(interval estimate):提供基于样本得出的点估计值与总体参数值的接近程度方面的信息
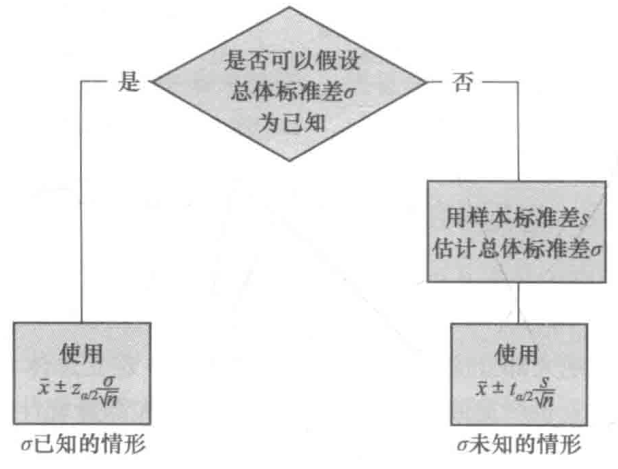
总体均值的区间估计:$\sigma$已知情形
置信水平(confidence level)
- 95%置信区间:任何正态分布随机变量都有95%的值在均值附近$\pm 1.96$个标准差以内
- 置信区间(confidence interval):区间估计的上下限包括的范围
- 置信系数(confidence coefficient):0.95
- 要想达到较高的置信水平,必须加大边际误差,即加大置信区间的宽度
- 区间估计的一般形式:$\bar{x}\pm z_{a/2}\frac{\sigma}{\sqrt{n} }$
其中,$1-a$为置信系数,$z_{a/2}$为标准正太概率分布上侧面积为$a/2$时的$z$值。
总体均值的区间估计:$\sigma$未知情形
当利用s估计$\sigma$时,边际误差和总体均值的区间估计都以t分布(t distribution)的概率为依据进行的。
t分布是由一类相似的概率分布组成的分布族,某个特定的t分布依赖于称为自由度(degrees of freedom)的参数。随着自由度的增大,t分布与标准正态分布之间的差别越来越小。
区间估计的一般形式:$\bar{x}\pm t_{a/2}\frac{s}{\sqrt{n} }$
总体均值区间估计中的样本容量:$n=\frac{(z_{a/2})^2\cdot \sigma ^2}{E^2}$
在总体分布严重偏斜时,应采用更大的样本容量。
总体比率的区间估计 :$\bar {p}\pm z_{a/2}\sqrt{\frac{\bar{p}(1-\bar{p})}{n} }$,其中,$1-a$为置信系数,$z_{a/2}$为标准正太分布上侧面积为$a/2$时的$z$值,边际误差是$z_{a/2}\sqrt{\bar{p}(1-\bar{p})/n}$。
总体比率区间估计的样本容量:$n=\frac{(z_{a/2})^2p^(1-p^)}{E^2}$,其中,$p^*$表示$\bar{p}$的计划值。
9 假设检验
原假设(null hypothesis,$H_{0}$):对总体参数做的尝试性假设。
- 将研究中的假设作为备择假设
- 将受到挑战的假说作为原假设
备择假设(alternative hypothesis,$H_{a}$):与原假设内容完全对立的假设。
| $H_{0}$是真的 | $H_{a}$是真的 | |
|---|---|---|
| 接受$H_{0}$ | 结论正确 | 第二类错误 |
| 拒绝$H_{0}$ | 第一类错误 | 结论正确 |
- 第一类错误(Type I error):当$H_{0}$为真,但我们拒绝时
- 第二类错误(Type II error):当$H_{0}$为假,但我们接受时
- 显著性水平$a$:当原假设为真并且以等式形式出现时,犯第一类错误的概率称为检验的显著性水平。一般取值为0.05和0.01
假设检验的步骤:

总体均值的检验:$\sigma$已知情形
样本选自服从正态分布的总体,或样本容量足够大的非正大分布时,检验方法有效。
单侧检验(one-tailed test)
| 下侧检验 | 上侧检验 |
|---|---|
| $H_{0}:\mu \ge \mu_{0}$ | $H_{0}:\mu \le \mu_{0}$ |
| $H_{a}:\mu \lt \mu_{0}$ | $H_{a}:\mu \gt \mu_{0}$ |
在$\sigma$已知的情形下对总体均值进行假设检验,用标准正态随机变量$z$作为检验统计量(test statistic),来确定$\bar{x}$是否偏离假定值$\mu$足够远,从而有理由拒绝原假设。
总体均值假设检验的检验统计量:$z=\frac{\bar{x}-\mu_{0}}{\sigma/\sqrt{n}}$。
下侧检验中,检验统计量$z$必须达到多小时,我们才能选择拒绝原假设。
- p-值法:度量样本所提供的证据对原假设的支持程度,越小说明拒绝原假设的证据越多
- 临界值法:如果$z\ge -z_{a}$,则拒绝$H_{0}$
双侧检验(two-tailed test)
双侧检验的一般形式:$H_{0}:\mu=\mu_{0}$,$H_{a}:\mu\ne \mu_{0}$。
- p值法
- 临界值法
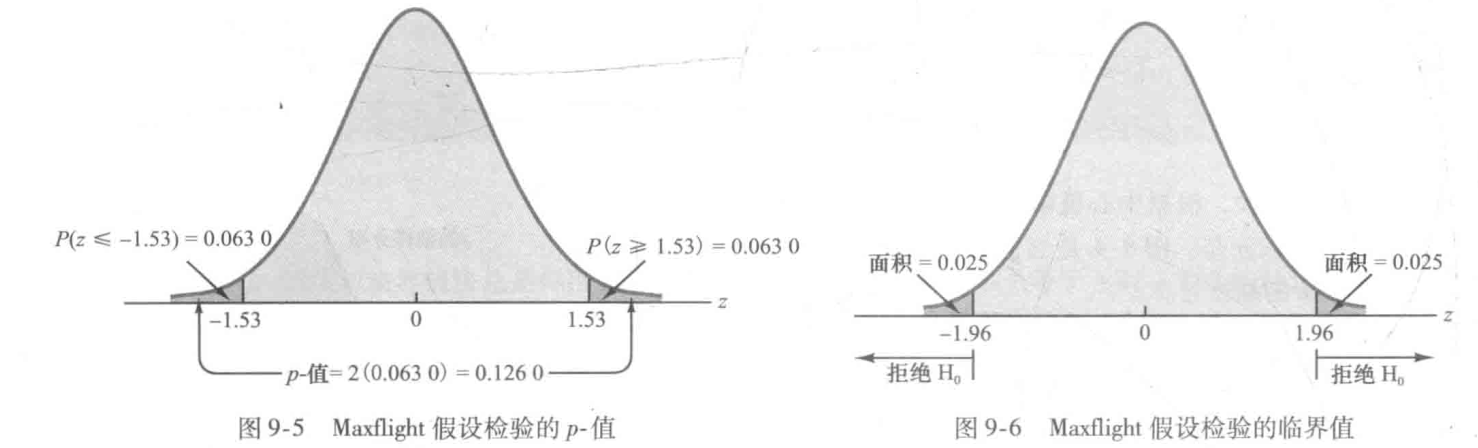
用置信区间的方法进行假设检验:

总体均值的检验:$\sigma$未知情形
总体均值假设检验的检验统计量:$z=\frac{\bar{x}-\mu_{0}}{s/\sqrt{n}}$。
总体比率的假设检验
总体比率假设检验的检验统计量:$z=\frac{\bar{p}-p_{0}}{\sqrt{\frac{P_{0}(1-P_{0})}{n}}}$。
检验的功效:当$H_{0}$为假时,得出拒绝$H_{0}$的正确结论的概率。值为:$1-第二类错误的概率$。
功效曲线:维持出与每一个$\mu$值相对应的功效。
总体均值单侧假设检验的样本容量:
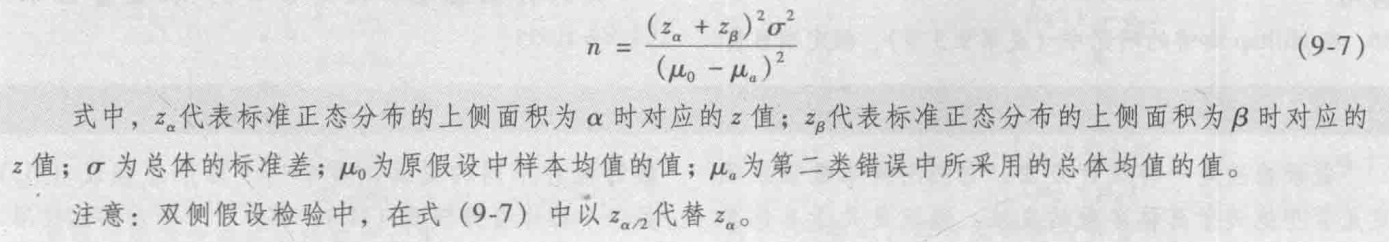
10 两总体均值和比例的推断
$\mu _{1}$:总体1的均值。
$\mu _{2}$:总体2的均值。
从总体1和总体2中分别抽出容量为$n_{1}$和$n_{2}$的独立简单随机样本。
总体1的均值-总体2的均值:$\mu _{1}- \mu _{2}$。
样本1的均值:$\bar{x} _{1}$。
样本2的均值:$\bar{x} _{2}$。
两个总体均值之差的点估计量:$\bar{x}{1}-\bar{x}{2}$。
$\bar{x}{1}-\bar{x}{2}$的标准误差:$\sigma_{\bar{x}{1}-\bar{x}{2}}=\sqrt{\frac{\bar{\sigma}{1}^2}{n{1}}+\frac{\bar{\sigma}{2}^2}{n{2}}}$。
两总体均值之差的推断:$\sigma _{1}$和$\sigma _{2}$已知
两个总体均值之差的区间估计:$\bar{x}{1}-\bar{x}{2} \pm 边际误差$,$边际误差=z_{a/2}\sigma_{\bar{x}{1}-\bar{x}{2}}=z_{a/2}\sqrt{\frac{\sigma_{1}^2}{n_{1}}+\frac{\sigma_{2}^2}{n_{2}}}$,其中,$1-a$为置信系数。
$\mu {1}-\mu _{2}$的假设检验的检验统计量:$z=\frac{(\bar{x}{1}-\bar{x}{2})-D{0}}{\sqrt{\frac{\sigma_{1}^2}{n_{1}}+\frac{\sigma_{2}^2}{n_{2}}}}$,其中$D_{0}$表示$\mu _{1}$与$\mu _{2}$之间假设的差。
两总体均值之差的推断:$\sigma _{1}$和$\sigma _{2}$未知
两个总体均值之差的区间估计:$\bar{x}{1}-\bar{x}{2} \pm 边际误差$,$z=\frac{(\bar{x}{1}-\bar{x}{2})-D_{0}}{\sqrt{\frac{s_{1}^2}{n_{1}}+\frac{s_{2}^2}{n_{2}}}}$,其中,$1-a$为置信系数。
$\mu {1}-\mu _{2}$的假设检验的检验统计量:$t=\frac{(\bar{x}{1}-\bar{x}{2})-D{0}}{\sqrt{\frac{s_{1}^2}{n_{1}}+\frac{s_{2}^2}{n_{2}}}}$,其中$D_{0}$表示$\mu _{1}$与$\mu _{2}$之间假设的差。
自由度:两个独立随机样本的t分布:$df=\frac{\left ( \frac{s_{1}^2}{n_{1}}+\frac{s_{2}^2}{n_{2}} \right )^2 }{\frac{1}{n_1-1}\left ( \frac{s_{1}^2}{n_{1}}\right ) ^2+\frac{1}{n_2-1}\left ( \frac{s_{2}^2}{n_{2}}\right ) ^2}$。
两总体均值之差的推断:匹配样本
- 独立样本设计:独立的两个总体中抽取
- 匹配样本设计:由相同的主体分别产生两个总体的数据
两总体比例之差的推断
两总体比例之差的点估计量:$p_1-P_2$。
$p_1-P_2$的标准误差:$\sigma_{\bar{p_1}-\bar{p_2}}=\sqrt{\frac{p_1(1-p_1)}{n_1}+\frac{p_2(1-p_2)}{n_2}}$。
两总体比例之差的区间估计:$\bar{p_1}-\bar{p_2}\pm z_{a/2}\sqrt{\frac{\bar{p}_1\left (1-\bar{p}_1 \right )}{n_1}+\frac{\bar{p}_2\left (1-\bar{p}_2 \right )}{n_2}}$。
11 总体方差的统计推断
$\chi ^2$分布:从正态总体中做生意抽取一个容量为n的简单随机样本,则$\frac{(n-1)s^2}{\sigma ^2}$的抽样分布服从自由度为n-1的$\chi ^2$分布。
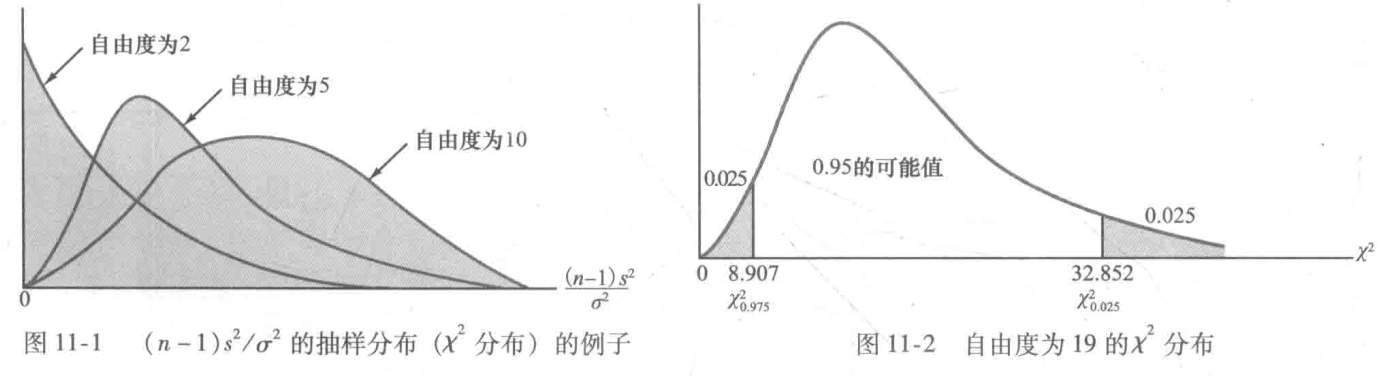
总体方差的区间估计:$\frac{(n-1)s^2}{\chi_{a/2}^2}\le \sigma^2\le\frac{(n-1)s^2}{\chi_{1-a/2}^2}$。
总体方差的假设检验的检验统计量:$\chi^2=\frac{(n-1)s^2}{\sigma_0^2}$。
两个总体方差的统计推断
从两个方差相等的正态总体中分别抽取容量为$n_1$,$n_2$的两个独立简单随机样本,两个样本方差$s_1^2$和$s_2^2$是推断总体方差$\sigma_1^2$和$\sigma_2^2$的基础。当$\sigma_1^2=\sigma_2^2$时,样本方差之比$\frac{s_1^2}{s_2^2}$服从分子自由度为$n_1-1$和分母自由度为$n_2-1$的F分布。
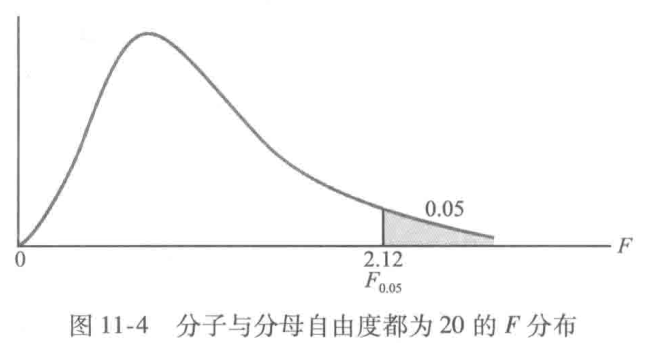
$\sigma_1^2=\sigma_2^2$的假设检验的检验统计量:$F=\frac{s_1^2}{s_2^2}$。
12 多个比例的比较、独立性及拟合优度检验
三个或多个总体比例的相等性的检验
检验统计量$\chi ^2$:$\chi^2=\sum_{i}\sum_{j}\frac{(f_{ij}-e_{ij})^2}{e_{ij}}$,其中,$f_{ij}$表示第i行和第j列的单元格的观察频数,$e_{ij}$表示在假定$H_0$为真时第i行和第j列的单元格的期望频数。
一般步骤如下:

多重比较方法:Marascuilo方法
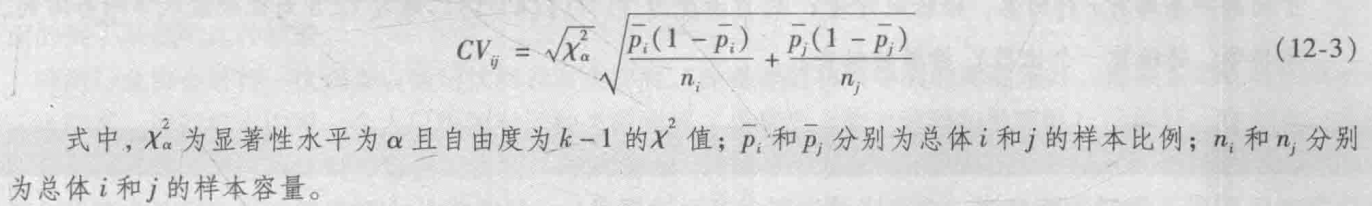
独立性检验
两个分类变量独立性的$\chi^2$检验:

拟合优度检验
确定一个被抽样的总体是否服从某个特殊的概率分布。
多项概率分布的拟合优度检验:

正态分布的拟合优度检验:


13 实验设计与方差分析
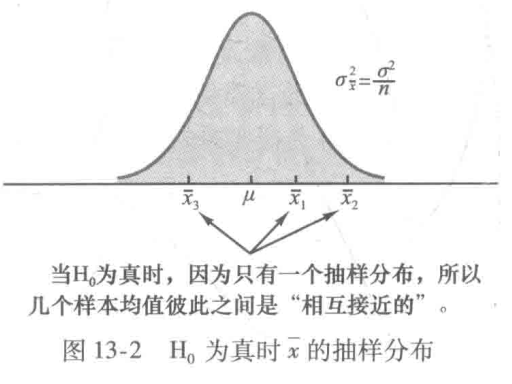
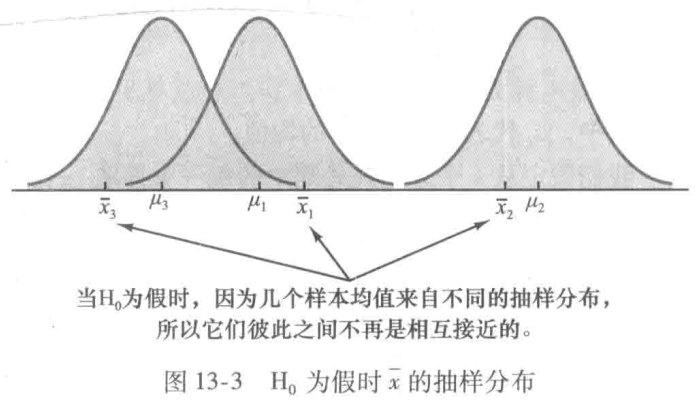
方差分析(ANOVA)的假定:
- 对每个总体,响应变量服从正态分布
- 响应变量的方差,对所有总体都是相同的
- 观测值必须是独立的
均方处理(mean square due to treatments,MSTR):$MSTR=\frac{\sum_{j=1}^{k}n_j(\bar x_j-\bar{\bar x} )^2 }{k-1}$,分子被称为处理平方和(sum of squares due to treatments,SSTR),分母$k-1$表示与SSTR相联系的自由度。
均方误差(mean square due to error,MSE):$MSE=\frac{\sum_{j=1}^{k} (n_j-1)s_j^2}{n_T-k}$。
方差估计量的比较,k个总体均值相等的检验统计量:F检验,$F=\frac{MSTR}{MSE}$,检验统计量服从分子自由度为$k-1$,分母自由度为$n_T-k$的F分布。

多重比较方法(multiple comparison procedures):确定在k个均值中哪几个均值之间存在差异。
Fisher的最小显著性差异(least significant difference,LSD)方法
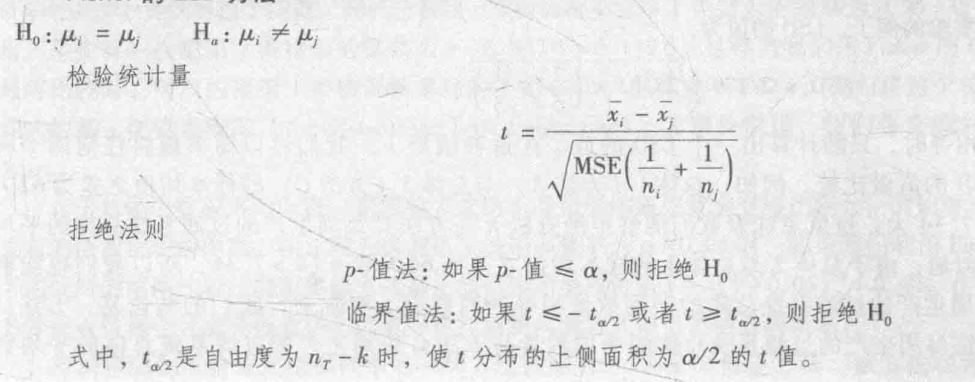


随机化区组设计
通过消除MSE项中来自外部的变异,达到控制变异外部来源的目的。为真实的误差方差给出了一个更好的估计。
析因实验
同时得到有关两个或两个以上因子同时存在的一些统计结论。
参考
版权声明:本文为博主原创文章,转载请注明出处。 旭日酒馆