概念
1.kNN(k-NearestNeighbor)
所谓K最近邻,就是k个最近的邻居的意思,说的是每个样本都可以用它最接近的k个邻居来代表。 kNN算法的核心思想是如果一个样本在特征空间中的k个最相邻的样本中的大多数属于某一个类别,则该样本也属于这个类别,并具有这个类别上样本的特性。
kNN在确定分类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。 kNN方法在类别决策时,只与极少量的相邻样本有关。由于kNN方法主要靠周围有限的邻近的样本,而不是靠判别类域的方法来确定所属类别的,因此对于类域的交叉或重叠较多的待分样本集来说,kNN方法较其他方法更为适合。
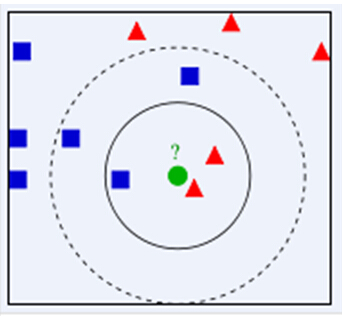
KNN本质是基于一种数据统计的方法,从图中我们可以看到,图中的数据集是良好的数据,即都打好了label,一类是蓝色的正方形,一类是红色的三角形,那个绿色的圆形是我们待分类的数据(绿色圆要被决定赋予哪个类,是红色三角形还是蓝色四方形?)如果K=3,由于红色三角形所占比例为2/3,绿色圆将被赋予红色三角形那个类,如果K=5,由于蓝色四方形比例为3/5,因此绿色圆被赋予蓝色四方形类。
KNN算法不仅可以用于分类,还可以用于回归。通过找出一个样本的k个最近邻居,将这些邻居的属性的平均值赋给该样本,就可以得到该样本的属性。更有用的方法是将不同距离的邻居对该样本产生的影响给予不同的权值(weight),如权值与距离成反比。
1 算法流程
- 准备数据,对数据进行预处理
- 选用合适的数据结构存储训练数据和测试元组
- 设定参数,如k
- 维护一个大小为k的的按距离由大到小的优先级队列,用于存储最近邻训练元组。随机从训练元组中选取k个元组作为初始的最近邻元组,分别计算测试元组到这k个元组的距离,将训练元组标号和距离存入优先级队列
- 遍历训练元组集,计算当前训练元组与测试元组的距离,将所得距离L 与优先级队列中的最大距离Lmax
- 进行比较。若L>=Lmax,则舍弃该元组,遍历下一个元组。若L < Lmax,删除优先级队列中最大距离的元组,将当前训练元组存入优先级队列。
- 遍历完毕,计算优先级队列中k 个元组的多数类,并将其作为测试元组的类别。
- 测试元组集测试完毕后计算误差率,继续设定不同的k值重新进行训练,最后取误差率最小的k 值。
2 优点
- 简单,易于理解,易于实现,无需估计参数,无需训练;
- 适合对稀有事件进行分类;
- 特别适合于多分类问题(multi-modal,对象具有多个类别标签), kNN比SVM的表现要好。
3 缺点
- 当样本不平衡时,如一个类的样本容量很大,而其他类样本容量很小时,有可能导致当输入一个新样本时,该样本的K个邻居中大容量类的样本占多数。 该算法只计算“最近的”邻居样本,某一类的样本数量很大,那么或者这类样本并不接近目标样本,或者这类样本很靠近目标样本。无论怎样,数量并不能影响运行结果。
- 该方法的另一个不足之处是计算量较大,因为对每一个待分类的文本都要计算它到全体已知样本的距离,才能求得它的K个最近邻点。
- 可理解性差,无法给出像决策树那样的规则。
4 改进策略
针对以上算法的不足,算法的改进方向主要分成了分类效率和分类效果两方面。
分类效率:事先对样本属性进行约简,删除对分类结果影响较小的属性,快速的得出待分类样本的类别。该算法比较适用于样本容量比较大的类域的自动分类,而那些样本容量较小的类域采用这种算法比较容易产生误分。
分类效果:采用权值的方法(和该样本距离小的邻居权值大)来改进,Han等人于2002年尝试利用贪心法,针对文件分类实做可调整权重的k最近邻居法WAkNN (weighted adjusted k nearest neighbor),以促进分类效果;而Li等人于2004年提出由于不同分类的文件本身有数量上有差异,因此也应该依照训练集合中各种分类的文件数量,选取不同数目的最近邻居,来参与分类。
2.代价函数(Cost Function)
在KNN中,通过计算对象间距离来作为各个对象之间的非相似性指标,避免了对象之间的匹配问题,通常使用欧氏距离或曼哈顿距离:
欧式距离:
\[d(x,y)=\sqrt{\sum_{k=1}^{n}(x_{k}-y_{k})^{2}}\]曼哈顿距离:
\[d(x,y)=\sqrt{\sum_{k=1}^{n}|x_{k}-y_{k}|}\]3.最小化J($\theta$)的方法
通过遍历查找误差最小的k值
scikit-learn示例
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
from sklearn import neighbors, datasets
n_neighbors = 15
# 与逻辑回归一样,导入iris数据集
iris = datasets.load_iris()
#只使用前两条特征,二维数据便于图形化
X = iris.data[:, :2]
y = iris.target
h = .02 # meshgrid横纵坐标步进。
# 创建颜色表
cmap_light = ListedColormap(['#FFAAAA', '#AAFFAA', '#AAAAFF'])
cmap_bold = ListedColormap(['#FF0000', '#00FF00', '#0000FF'])
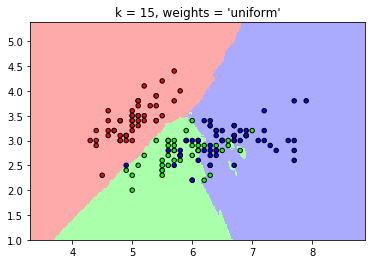
#uniform: 各点权重相同
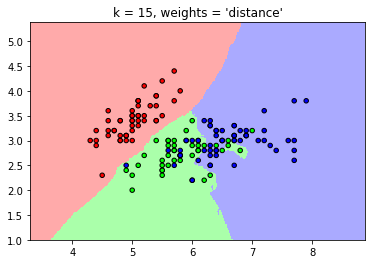
#distance: 距离近的权重大,远的权重小,分别以这两种方式应用算法
for weights in ['uniform', 'distance']:
# knn算法.
clf = neighbors.KNeighborsClassifier(n_neighbors, weights=weights)
clf.fit(X, y)
# meshgrid函数用两个坐标轴上的点在平面上画网格,此处用于画出分类的边界
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
np.arange(y_min, y_max, h))
#预测值并在图上画出边界
Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
plt.figure()
plt.pcolormesh(xx, yy, Z, cmap=cmap_light)
# 画出训练集的实际位置
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=cmap_bold,
edgecolor='k', s=20)
plt.xlim(xx.min(), xx.max())
plt.ylim(yy.min(), yy.max())
plt.title("k = %i, weights = '%s'"
% (n_neighbors, weights))
plt.show()
版权声明:本文为博主原创文章,转载请注明出处。 旭日酒馆