概念
1.逻辑回归(Logistic Regression)
对于Logistic Regression来说,其思想也是基于线性回归(Logistic Regression属于广义线性回归模型)。其公式如下:
\[h_{\theta }=\frac{1}{1+\epsilon ^{-z}}=\frac{1}{1+\epsilon ^{-\theta ^{T}x}}\]其中 $y=\frac{1}{1+\epsilon ^{-x}}$称作sigmoid函数,我们可以看到,Logistic Regression算法是将线性函数的结果映射到了sigmoid函数中。
sigmoid的函数图形如下:
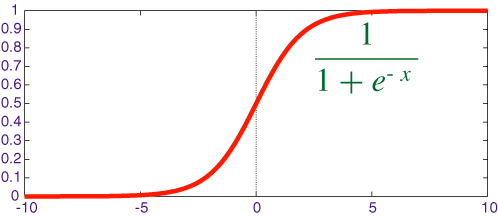
我们可以看到,sigmoid的函数输出是介于(0,1)之间的,中间值是0.5,于是之前的公式 h_{\theta }(x) 的含义就很好理解了,因为h_{\theta }(x) 输出是介于(0,1)之间,也就表明了数据属于某一类别的概率,例如 :
- hθ(x)<0.5 则说明当前数据属于A类
- hθ(x)>0.5 则说明当前数据属于B类
所以我们可以将sigmoid函数看成样本数据的概率密度函数。
那么,怎样去估计参数θ呢,θ的值表示 h_{\theta }(x) 结果取1的概率,因此对于输入x分类结果为类别1和类别0的概率分别为:
\[P(y=1|x;\theta )=h_{\theta }(x)\] \[P(y=0|x;\theta )=1-h_{\theta }(x)\]
2.代价函数(Cost Function)
\[cost(h^{_{\theta }},y)=\left\{\begin{matrix} -log(h_{\theta }(x)) & if y=1 \\ -log(1-h_{\theta }(x)) & if y=0 \end{matrix}\right.\]这个损失函数,也叫作对数似然损失函数:
- 当y=1时,假定这个样本为正类。如果此时h_{\theta }(x)=1,则单对这个样本而言的cost=0,表示这个样本的预测完全准确。那如果所有样本都预测准确,总的cost=0
-
但是如果此时预测的概率h_{\theta }(x)=0,那么cost→∞。直观解释的话,由于此时样本为一个正样本,但是预测的结果P(y=1 x;θ)=0,也就是说预测 y=1的概率为0,那么此时就要对损失函数加一个很大的惩罚项。 - 当y=0时,推理过程跟上述完全一致。
将以上两个表达式合并为一个,则单个样本的损失函数可以描述为:
\[cost(h_{\theta }(x),y)=-y_{i}log(h_{\theta }(x))-(1-y_{i})log(1-h_{\theta }(x))\]因为 yi 只有两种取值情况,1或0,分别令y=1或y=0,即可得到原来的分段表示式。
全体样本的损失函数即逻辑回归最终的损失函数表达式可以表示为:
\[cost(h_{\theta }(x),y)=\sum_{i=1}^{m}-y_{i}log(h_{\theta }(x))-(1-y_{i})log(1-h_{\theta }(x))\]3.最小化J($\theta$)的方法
逻辑回归与线性回归形式相近,同样使用梯度下降法(gradient descent)
常用损失函数
1. 0-1损失函数 (0-1 loss function)
\[L(Y,f(X))=\left\{\begin{matrix}1,Y\neq f(X)) \\ 0,Y= f(X)) \end{matrix}\right.\]2. 平方损失函数(quadratic loss function)
\[L(Y,f(X))=(Y-f(X))^{2}\]3. 绝对值损失函数(absolute loss function)
\[L(Y,f(x))=|Y-f(X)|\]4. 对数损失函数(logarithmic loss function) 或对数似然损失函数(log-likehood loss function)
\[L(Y,P(Y|X))=-logP(Y|X)\]逻辑回归的损失函数
逻辑回归和线性回归形式相近,为什么不模仿线性回归的做法,利用误差平方和来当代价函数呢,由于逻辑回归的损失函数是__非凸的__,无法找到全局最优解。
逻辑回归采用对数损失函数。在逻辑回归的推导中,我们假设样本是服从伯努利分布(0-1分布)的,然后求得满足该分布的似然函数,最终求该似然函数的极大值。整体的思想就是求极大似然函数的思想。取对数是求MLE(Maximum Likelihood Estimation)过程中采取的一种数学手段。
cost function和lostfunction
简单说,loss function是对于单个样本而言的,比如对于0-1分类问题,当前预测样本x的输出为t,实际值为y,那么loss function就是y-t,或者abs(y-t);对于连续型数据的预测,也就是回归问题,loss function可以是差值的平方:(y-t)^2
而cost function是对于样本总体而言的,对于0-1分类问题,loss function是n个样本的loss function取值的均值;而对于回归问题,cost function是n个样本的平方误差的平均,俗称均方误差(mean square error)
总的来说cost function是各个样本的loss funcion的平均
另外还有error,一个预测结果和实际标签比较,一样的话不算错,不一样就算错(仅考虑分类问题)。 那么我在一个miniBatch之内,比如100张图,每张图对应一个分类的标签,以及一个预测出来的结果,这个预测结果和标签做比较,如果不一致说明“预测错了”。统计所有100张图上“预测错误的结果”的数量,比如有3个,那么error就认为是3,或者表示为3%。
也就是说,error表示的是“累计错误数量的占比”。从这一点来看,error关注的是“是否正确”的累计,而不是“单个结果上错误的程度”,error关注的是“质”,而loss关注的是“错误的程度”(根据loss函数来决定),这一点上,error和loss是有所不同的。
4.优化
除了的梯度下降算法之外,还有一些叫做共轭梯度下降算法(BFGS,L-BFGS)。使用这些共轭梯度下降算法的好处在于,不需要手动地选择学习率a,这些算法会自行尝试选择a;比梯度下降算法运算更快。
一般情况下,在常见的机器学习算法库中都带有这些算法。
- 多类别分类问题
现实世界中除了二元的分类问题还有多元的分类问题,如对天气的分类,是晴天、多云、小雨等等天气。 多元分类问题,不同与二元分类问题,这类问题把结果分为n>2类。这样n元的分类问题,就需要进行n次的机器学习。对每一次的分类结果记为h(x)。那么经过n此分类之后,最后得到的结果为:
\[h_{\theta }^{(i))}=P(y=i|x;\theta )\] \[(i=1,2,3...)\]最大似然估计
参数估计问题只是实际问题求解过程中的一种简化方法(由于直接估计类条件概率密度函数很困难)。所以能够使用极大似然估计方法的样本必须需要满足一些前提假设。
- 训练样本的分布能代表样本的真实分布
- 每个样本集中的样本都是所谓独立同分布的随机变量 (iid条件),且有充分的训练样本
 。
。
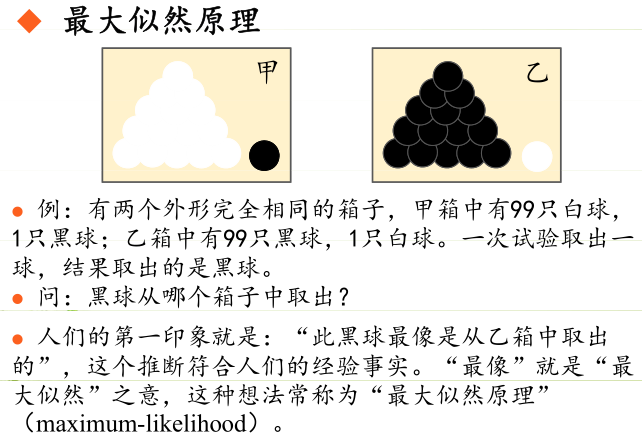
最大似然估计是建立在极大似然原理的基础上的一个统计方法,是概率论在统计学中的应用。极大似然估计提供了一种给定观察数据来评估模型参数的方法,即:“模型已定,参数未知”。通过若干次试验,观察其结果,利用试验结果得到某个参数值能够使样本出现的概率为最大,则称为极大似然估计。
scikit-learn示例
from sklearn import datasets,linear_model
import numpy as np
from sklearn.cross_validation import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import accuracy_score
import matplotlib.pyplot as plt
iris = datasets.load_iris() # scikit-learn自带数据集,Iris有4个特征,3个类别。但是,我们为了数据的可视化,我们只保留2个特征(sepal length和petal length)。
X = iris.data[:, [2, 3]]
y = iris.target # 标签已经转换成0,1,2了
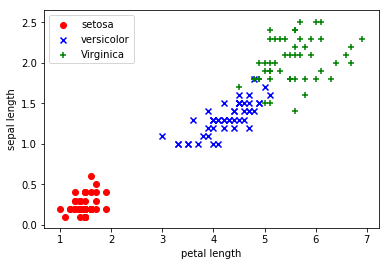
#直观观察数据分布
plt.scatter(X[:50, 0], X[:50, 1],color='red', marker='o', label='setosa') # 前50个样本的散点图
plt.scatter(X[50:100, 0], X[50:100, 1],color='blue', marker='x', label='versicolor') # 中间50个样本的散点图
plt.scatter(X[100:, 0], X[100:, 1],color='green', marker='+', label='Virginica') # 后50个样本的散点图
plt.xlabel('petal length')
plt.ylabel('sepal length')
plt.legend(loc=2) # 把说明放在左上角
plt.show()
# 切分测试集和训练集,随机拿出数据集中20%的部分做测试
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)
# 为了得到最佳性能,我们将特征缩放
sc = StandardScaler()
sc.fit(X_train) # 估算每个特征的平均值和标准差
print("mean:%s" % sc.mean_) # 2个特征的平均值
print("std:%s" % sc.scale_) # 特征的标准差
# 用同样的参数标准化测试集和训练集
X_train_std = sc.transform(X_train)
X_test_std = sc.transform(X_test)
#用逻辑回归分类
classifer = linear_model.LogisticRegression()
classifer.fit(X_train_std,y_train)
#系数
print("coefficients:",classifer.coef_)
#截矩
print("intercept:",classifer.intercept_)
# 分类测试集,这将返回一个测试结果的数组
y_pred = classifer.predict(X_test_std)
# 计算模型在测试集上的准确性
print("accuracy_score:%s"% accuracy_score(y_test, y_pred))
#测试结果和实际结果的对比图
print("y_test:" ,y_test)
print("y_pred:",y_pred)
mean:[3.81583333 1.23083333]
std:[1.77745116 0.7732826 ]
coefficients: [[-2.18277467 -1.81282216]
[ 1.17215267 -0.92165247]
[ 1.77505729 2.50775931]]
intercept: [-1.98359067 -0.79955622 -2.16804839]
accuracy_score:0.7666666666666667
y_test: [2 1 0 2 0 2 0 1 1 1 2 1 1 1 1 0 1 1 0 0 2 1 0 0 2 0 0 1 1 0]
y_pred: [2 1 0 2 0 2 0 2 1 1 1 2 1 2 1 0 2 1 0 0 2 2 0 0 2 0 0 1 0 0]
其中,classifer.coef_ (以特征数量为列,以分类后结果数量为行) ,和classifer.intercept_为回归得出的系数及截矩. 本例中,有2个特征数量x1,x2,相应地有两个系数w0,w1,结果集y中共有0,1,2三类,所以有3个intercept。具体关系如下:
| y | w0 | w1 | intercept |
|---|---|---|---|
| 0 | -2.18277467 | -1.81282216 | -1.98359067 |
| 1 | 1.17215267 | -0.92165247 | -0.79955622 |
| 2 | 1.77505729 | 2.50775931] | -2.16804839 |
版权声明:本文为博主原创文章,转载请注明出处。 旭日酒馆