概念
DNN可以理解为有很多隐藏层的神经网络, 多层神经网络和深度神经网络DNN其实也是指的一个东西,DNN有时也叫做多层感知机(Multi-Layer perceptron,MLP), 从DNN按不同层的位置划分,DNN内部的神经网络层可以分为三类,输入层,隐藏层和输出层,如下图示例,一般来说第一层是输入层,最后一层是输出层,而中间的层数都是隐藏层。
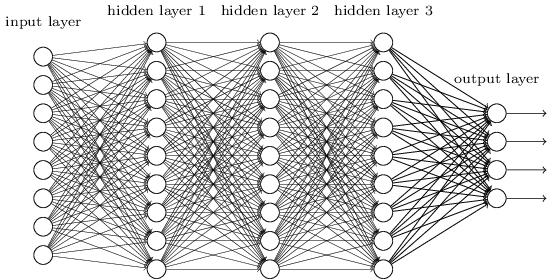
层与层之间是全连接的,也就是说,第i层的任意一个神经元一定与第i+1层的任意一个神经元相连。虽然DNN看起来很复杂,但是从小的局部模型来说,还是和感知机一样,即一个线性关系$z=\sum w_{i}x_{i}+b$加上一个激活函数σ(z)。
常见响应函数(非线性函数)
logistic/sigmoid function:
\[f(z)=\frac{1}{1+exp(-z)}\]tanh
\[f(z)=tanh(z)=\frac{e^{z}-e^{-z}}{e^{z}+e^{-z}}\]step/binary functional
if u>=$\theta$ y=1
if u<$\theta$ y=0
rectifier function
f(x)=max(0,x)
analytic function:rectifier function的平滑近似:
\[f(x)=ln(1+e^{x})\]反向传播算法(back propagation)
深度学习的训练是成本函数(cost function)最小化的过程,一般采取梯度下降法求解。那么怎么计算梯度呢?这就要用到back propagation了。计算一个数学表达式的梯度是很直接的,但计算代价昂贵。而反向传播算法使用简单的方法有效地减少了计算量。
反向传播经常被误解为神经网络的整个学习算法。而实际上,反向传播仅用于计算梯度,然后另一种算法(如随机梯度下降SGD)利用反向传播得到的梯度进行学习。
以求f(x,y,z)=(x+y)z 的偏导为例:
引入一个中间变量q,将公式分成两部分:q=x+y 和 f=qz:
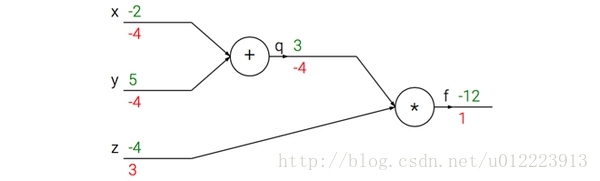
上图的真实值计算线路展示了计算的视觉化过程。前向传播从输入计算到输出(绿色),反向传播从尾部开始,根据链式法则递归地向前计算梯度(显示为红色),一直到网络的输入端。可以认为,梯度是从计算链路中回流。
利用链式法则我们知道:
\[\frac{\partial f}{\partial x}=\frac{\partial f}{\partial q}\frac{\partial q}{\partial x}\]在实际操作中,这只是简单地将两个梯度数值相乘。反向传播从尾部开始,根据链式法则递归地向前计算梯度。
以上图为例,反向传播从从最上层的节点f开始,初始值为1,以层为单位进行处理。节点q接受f发送的1并乘以该节点的偏导值-4等于-4,节点z接受f发送的1并乘以该节点的偏导值3等于3,至此第二层完毕,求出各节点总偏导值并继续向下一层发送。节点q向x发送-4并乘以偏导值1等于-4,节点q向y发送-4并乘以偏导值1等于-4,至此第三层完毕,节点x,y的偏导值都为-4,即顶点f对x,y的偏导数均为-4.
实际上,反向传播就是梯度下降法中链式法则的使用。
版权声明:本文为博主原创文章,转载请注明出处。 旭日酒馆