概念
循环神经网络(Recurrent Neural Networks ,以下简称RNN),广泛的用于自然语言处理中的语音识别,手写书别以及机器翻译等领域。
RNN假设我们的样本是基于序列的。比如是从序列索引1到序列索引τ的。对于这其中的任意序列索引号t,它对应的输入是对应的样本序列中的x(t)。而模型在序列索引号t位置的隐藏状态h(t),则由x(t)和在t−1位置的隐藏状态h(t−1)共同决定。在任意序列索引号t,我们也有对应的模型预测输出o(t)。通过预测输出o(t)和训练序列真实输出y(t),以及损失函数L(t),我们就可以用DNN类似的方法来训练模型,接着用来预测测试序列中的一些位置的输出。
RNN模型
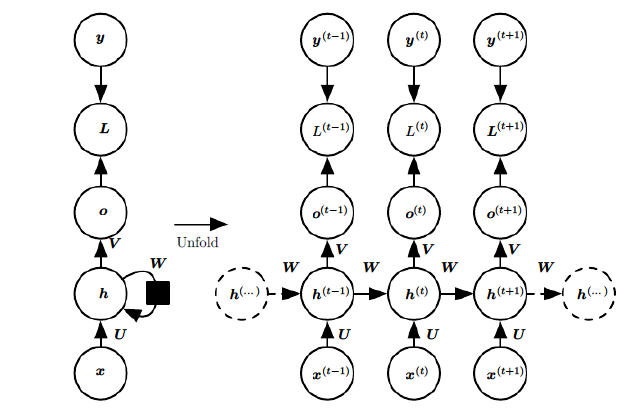
上图中左边是RNN模型没有按时间展开的图,如果按时间序列展开,则是上图中的右边部分。我们重点观察右边部分的图。
这幅图描述了在序列索引号t附近RNN的模型。其中:
-
x(t)代表在序列索引号t时训练样本的输入。同样的,x(t−1)和x(t+1)代表在序列索引号t−1和t+1时训练样本的输入。
-
h(t)代表在序列索引号t时模型的隐藏状态。h(t)由x(t)和h(t−1)共同决定。
-
o(t)代表在序列索引号t时模型的输出。o(t)只由模型当前的隐藏状态h(t)决定。
-
L(t)代表在序列索引号t时模型的损失函数。
-
y(t)代表在序列索引号t时训练样本序列的真实输出。
-
U,W,V这三个矩阵是我们的模型的线性关系参数,它在整个RNN网络中是共享的,这点和DNN不同。 也正因为是共享了,它体现了RNN的模型的“循环反馈”的思想。
LSTM
由于RNN也有梯度消失的问题,因此很难处理长序列的数据,RNN的特例LSTM(Long Short-Term Memory),可以避免常规RNN的梯度消失,因此在工业界得到了广泛的应用。
对于上图的RNN模型,如果略去每层都有的o(t),L(t),y(t),则RNN的模型可以简化成如下图的形式:
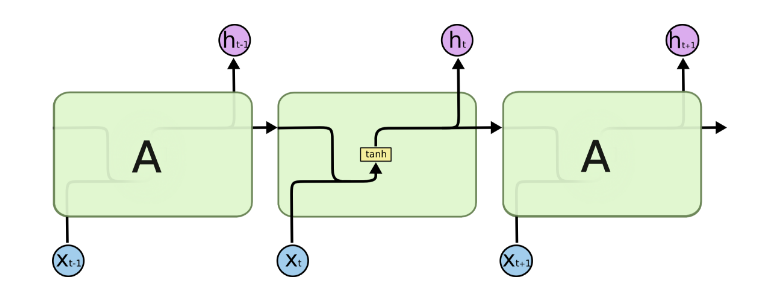
图中可以看出在隐藏状态h(t)由x(t)和h(t−1)得到。得到h(t)后一方面用于当前层的模型损失计算,另一方面用于计算下一层的h(t+1)。
由于RNN梯度消失的问题,对序列索引位置t的隐藏结构做改进来避免梯度消失的问题,这样的特殊RNN就是我们的LSTM。由于LSTM有很多的变种,这里我们以最常见的LSTM为例讲述。LSTM的结构如下图:
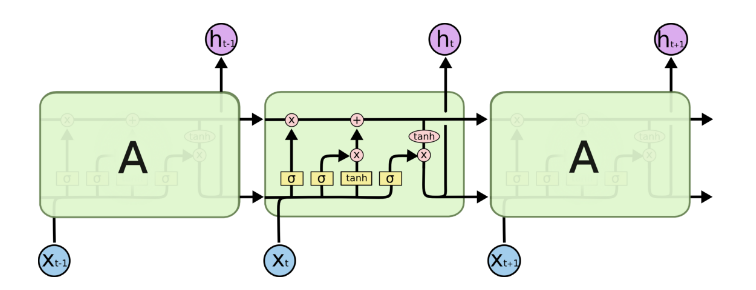
LSTM细胞状态(Cell State)
在每个序列索引位置t时刻向前传播的除了和RNN一样的隐藏状态h(t),还多了另一个隐藏状态,如图中上面的长横线。这个隐藏状态我们一般称为细胞状态,记为C(t)
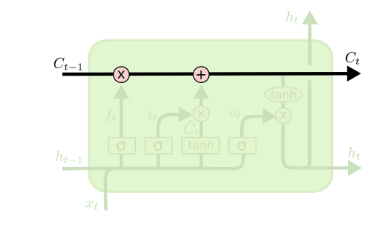
LSTM门控结构(Gate)
LSTM在在每个序列索引位置t的门一般包括遗忘门,输入门和输出门三种。下面我们就来研究上图中LSTM的遗忘门,输入门和输出门以及细胞状态。
- 遗忘门 遗忘门(forget gate)是控制是否遗忘的,在LSTM中即以一定的概率控制是否遗忘上一层的隐藏细胞状态。遗忘门子结构如下图所示:
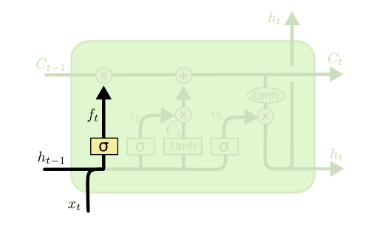
图中输入的有上一序列的隐藏状态h(t−1)和本序列数据x(t),通过一个激活函数,一般是sigmoid,得到遗忘门的输出f(t)。由于sigmoid的输出f(t)在[0,1]之间,因此这里的输出$f^{(t)}$代表了遗忘上一层隐藏细胞状态的概率。用数学表达式即为:
\[f^{(t)}=\sigma (W_{f}h^{(t-1)}+U_{f}x^{(t)}+b_{f})\]其中Wf,Uf,bf为线性关系的系数和偏倚,和RNN中的类似。σ为sigmoid激活函数。
- 输入门 输入门(input gate)负责处理当前序列位置的输入,它的结构如下图:
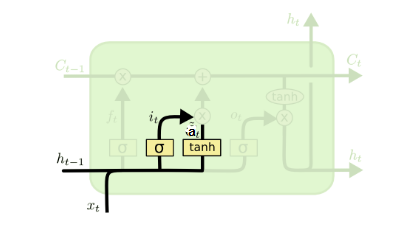
从图中可以看到输入门由两部分组成,第一部分使用了sigmoid激活函数,输出为i(t),第二部分使用了tanh激活函数,输出为a(t), 两者的结果后面会相乘再去更新细胞状态。用数学表达式即为:
\[i^{(t)}=\sigma (W_{i}h^{(t-1)}+U_{i}x^{(t)}+b_{i})\] \[a^{(t)}=tanh (W_{a}h^{(t-1)}+U_{a}x^{(t)}+b_{a})\]其中Wi,Ui,bi,Wa,Ua,ba,为线性关系的系数和偏倚,和RNN中的类似。σ为sigmoid激活函数。
遗忘门和输入门的结果都会作用于细胞状态C(t)。从细胞状态C(t−1)得到C(t)。如下图所示:
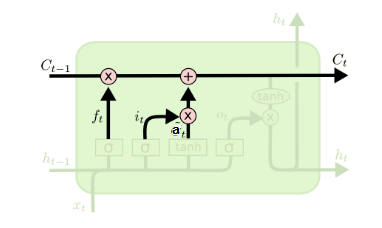
细胞状态C(t)由两部分组成,第一部分是C(t−1)和遗忘门输出f(t)的乘积,第二部分是输入门的i(t)和a(t)的乘积,即:
\[C^{(t)}=C^{(t-1)}\odot f^{(t)}+i^{(t)}\odot a^{(t)}\]其中,⊙为Hadamard积。
- 输出门
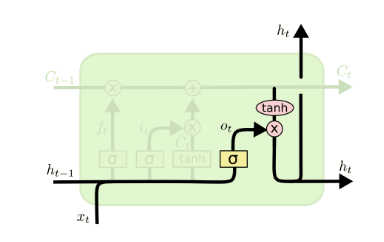
从图中可以看出,隐藏状态h(t)的更新由两部分组成,第一部分是o(t), 它由上一序列的隐藏状态h(t−1)和本序列数据x(t),以及激活函数sigmoid得到,第二部分由隐藏状态C(t)和tanh激活函数组成, 即:
\[o^{(T)}=\sigma (W_{o})h^{(t-1)}+U_{o}x^{(t)}+b_{o}\] \[h^{(t)}=o^{(t)}\odot tanh(C^{(t)})\]代码示例
#RNN
import torch
from torch import nn, optim
from torch.autograd import Variable
from torch.utils.data import DataLoader
from torchvision import transforms
from torchvision import datasets
# 定义超参数
batch_size = 100
learning_rate = 1e-3
num_epoches = 5
# MNIST 手写数字训练集
train_dataset = datasets.MNIST(
root='./data', train=True, transform=transforms.ToTensor(), download=True)
test_dataset = datasets.MNIST(
root='./data', train=False, transform=transforms.ToTensor())
train_loader = DataLoader(train_dataset, batch_size=batch_size, shuffle=True)
test_loader = DataLoader(test_dataset, batch_size=batch_size, shuffle=False)
# 定义 RNN 模型
class Rnn(nn.Module):
def __init__(self, in_dim, hidden_dim, n_layer, n_class):
super(Rnn, self).__init__()
self.n_layer = n_layer
self.hidden_dim = hidden_dim
self.lstm = nn.LSTM(in_dim, hidden_dim, n_layer, batch_first=True)
self.classifier = nn.Linear(hidden_dim, n_class)
def forward(self, x):
# h0 = Variable(torch.zeros(self.n_layer, x.size(1),
# self.hidden_dim)).cuda()
# c0 = Variable(torch.zeros(self.n_layer, x.size(1),
# self.hidden_dim)).cuda()
out, _ = self.lstm(x)
out = out[:, -1, :]
out = self.classifier(out)
return out
model = Rnn(28, 128, 2, 10) # 图片大小是28x28
use_gpu = torch.cuda.is_available() # 判断是否有GPU加速
if use_gpu:
model = model.cuda()
# 定义loss和optimizer
criterion = nn.CrossEntropyLoss()
optimizer = optim.Adam(model.parameters(), lr=learning_rate)
for epoch in range(num_epoches):
print('epoch {}'.format(epoch + 1))
print('*' * 10)
running_loss = 0.0
running_acc = 0.0
for i, data in enumerate(train_loader, 1):
img, label = data
b, c, h, w = img.size()
assert c == 1, 'channel must be 1'
img = img.squeeze(1)
# img = img.view(b*h, w)
# img = torch.transpose(img, 1, 0)
# img = img.contiguous().view(w, b, -1)
if use_gpu:
img = Variable(img).cuda()
label = Variable(label).cuda()
else:
img = Variable(img)
label = Variable(label)
# 向前传播
out = model(img)
loss = criterion(out, label)
running_loss += loss.data[0] * label.size(0)
_, pred = torch.max(out, 1)
num_correct = (pred == label).sum()
running_acc += num_correct.data[0]
# 向后传播
optimizer.zero_grad()
loss.backward()
optimizer.step()
if i % 300 == 0:
print('[{}/{}] Loss: {:.6f}, Acc: {:.6f}'.format(
epoch + 1, num_epoches, running_loss / (batch_size * i),
running_acc / (batch_size * i)))
print('Finish {} epoch, Loss: {:.6f}, Acc: {:.6f}'.format(
epoch + 1, running_loss / (len(train_dataset)), running_acc / (len(
train_dataset))))
model.eval()
eval_loss = 0.
eval_acc = 0.
for data in test_loader:
img, label = data
b, c, h, w = img.size()
assert c == 1, 'channel must be 1'
img = img.squeeze(1)
# img = img.view(b*h, w)
# img = torch.transpose(img, 1, 0)
# img = img.contiguous().view(w, b, h)
if use_gpu:
img = Variable(img, volatile=True).cuda()
label = Variable(label, volatile=True).cuda()
else:
img = Variable(img, volatile=True)
label = Variable(label, volatile=True)
out = model(img)
loss = criterion(out, label)
eval_loss += loss.data[0] * label.size(0)
_, pred = torch.max(out, 1)
num_correct = (pred == label).sum()
eval_acc += num_correct.data[0]
print('Test Loss: {:.6f}, Acc: {:.6f}'.format(eval_loss / (len(
test_dataset)), eval_acc / (len(test_dataset))))
print()
# 保存模型
torch.save(model.state_dict(), './rnn.pth')
epoch 1
**********
[1/5] Loss: 0.802155, Acc: 0.727267
[1/5] Loss: 0.507337, Acc: 0.831167
Finish 1 epoch, Loss: 0.507337, Acc: 0.831167
Test Loss: 0.151764, Acc: 0.955300
epoch 2
**********
[2/5] Loss: 0.142939, Acc: 0.955567
[2/5] Loss: 0.126432, Acc: 0.960967
Finish 2 epoch, Loss: 0.126432, Acc: 0.960967
Test Loss: 0.108675, Acc: 0.967300
epoch 3
**********
[3/5] Loss: 0.082724, Acc: 0.975033
[3/5] Loss: 0.079244, Acc: 0.975833
Finish 3 epoch, Loss: 0.079244, Acc: 0.975833
Test Loss: 0.072914, Acc: 0.978000
epoch 4
**********
[4/5] Loss: 0.057983, Acc: 0.981867
[4/5] Loss: 0.058047, Acc: 0.981950
Finish 4 epoch, Loss: 0.058047, Acc: 0.981950
Test Loss: 0.070141, Acc: 0.979400
epoch 5
**********
[5/5] Loss: 0.052662, Acc: 0.983267
[5/5] Loss: 0.049733, Acc: 0.984483
Finish 5 epoch, Loss: 0.049733, Acc: 0.984483
Test Loss: 0.058988, Acc: 0.981700
版权声明:本文为博主原创文章,转载请注明出处。 旭日酒馆